Introduction to Optical Design
A network planner needs to optimize the various electrical and optical parameters to ensure smooth operations of a wavelength division multiplexing (WDM) network. Whether the network topology is that of a point-to-point link, a ring, or a mesh, system design inherently can be considered to be of two separate parts: optical system design and electrical or higher-layer system design. To the networking world, the optical layer (WDM layer) appears as a barren physical layer whose function is to transport raw bits at a high bit rate with negligible loss. Most conventional network layer planners do not care about the heuristics of the optical layer.
However, such lapses can often be catastrophic. Until the bit rate and the transmission distance is under some bounded constraint (for example, small networks), it is often not important to consider the optical parameters.
However, as the bit rate increases and transmission length increases, these optical parameters have the capability of playing truant in the network. A network planner must consider the affecting parameters and build a network that accommodates the impairments caused by the optical parameters. This chapter explores some of the design constraints involved in the WDM network design.
Consider an optical signal as a slowly varying signal of amplitude A (τ, t) (function of distance 'τ' and time 't'), on which various parameters are acting at all times. An optical signal, as discussed in Chapter 1, "Introduction to Optical Networking," propagates through a silica fiber with propagation constant β, whose value is obtained from the solution of the basic wave equations. Further, this optical signal is subjected to attenuation, which by virtue of itself, is a property of the propagating medium—silica fiber in this case. Attenuation in a fiber is characterized by the attenuation constant α, which gives the loss (in dB) per traveled km.
Why is attenuation parameter important? First, common thinking says that if the total accumulated attenuation is greater than the signal input launch power Pin, a signal will not exist at the receiving end. This, although colloquial, is an important issue for verifying signal reception at the receiving end of a communication channel. Second, for optical communication to happen, a receiver (essentially a photodetector, either a PIN or APD type) needs a minimum amount of power to distinguish the 0s and 1s from the raw input optical signal.
The minimum power requirement of the receiver is called the receiver sensitivity, R, and is covered in Chapter 2, "Networking with DWDM-1." Here, we must ensure that the transmit power is high enough so that it can maintain signal power > R at the receiver end, despite the attenuation along the transmission line. That does not mean that if we increase the transmit power to a high level, we can send bits across great distances. High input power also is a breeding ground for impairments (nonlinearities such as cross-phase modulation [XPM], self-phase modulation [SPM], four-wave mixing [FWM] and so on). In addition, an upper limit exists for every receiver (APD type or PIN type) for receiving optical power. This is given by the dynamic range of the receiver, and it sets the maximum and minimum power range for the receiver to function. For example, –7 dBm to –28 dBm is a typical dynamic range of a receiver. Therefore, the maximum input power that we can launch into the fiber is limited. This also limits the maximum transmission distance, L. If PinMax is the maximum input power, the transmission distance is L, and Pr is the minimum receiver power; then Equation 4-1 shows the maximum input power that can be sent into the fiber and Equation 4-2 shows the maximum transmission distance.
Equation 4-1
![]()
Equation 4-2
![]()
NOTE
The optical power at the receiver end has to be within the dynamic range of the receiver; otherwise, it damages the receiver (if it exceeds the maximum value) or the receiver cannot differentiate between 1s and 0s if the power level is less than the minimum value.
For an input power of +5 dB and a receiver sensitivity of –20 dBm at 1550 nm, the maximum transmission distance without amplification is shown in the following equation. (Assume α = 0.2 dB/km at 1550 nm. We usually get α from the manufacture's spec.)
![]() (Here we neglected all other losses.)
(Here we neglected all other losses.)
Further in the preceding calculation, we have neglected dispersion, fiber nonlinearities, polarization, spectral broadening, chirp (source broadening), fiber plant losses (connecters, splices, and aging factors), and so on. If we consider these effects, then the maximum length is reduced further. How can we then have ultra long-haul intercontinental systems? By placing repeaters in cascade, we can enhance the transmission distance.
Two kinds of repeaters exist: opto-electro-opto (OEO) electrical repeaters that detect, reshape, retime, and retransmit (3R) the signal (channel-by-channel), and the fiber amplifiers (1R)(doped fiber, Raman, and SOA) that boost the signal power level (no reshape and no retiming) entirely in the optical domain. A third technique also exists: reshape and reamplify (2R) regeneration. This technique is gaining in popularity due to its protocol independence. This book discussed 2R in Chapter 2, so it is not necessary to consider it here from a design perspective because it proposes a generic alternative to the other design schemes.
Electrical repeaters have an advantage in that they can completely relaunch the signal by regenerating and further retransmitting it due to opto-electronic conversion and regeneration. To do so, the composite WDM signal needs to be fully demultiplexed, which is neither cost effective nor efficient. Optical amplifiers alleviate that problem by amplifying all the channels together completely in the optical domain; therefore, optical amplifiers can enhance the transmission distance. So, does that mean that optical amplifiers can increase the amplifying distance as much as they wants? Not really! Amplifiers come at a price and induct a trade off; they enhance the signal power level, but at the same time, they add their own complement of noise. This noise is amplified spontaneous emission (ASE), which was introduced in Chapter 3, "Networking with DWDM -2." Please refer to Figure 4-1.
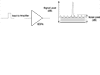 Figure 4-1 Single
Stage Amplifier and Noise Associated with Signal
Figure 4-1 Single
Stage Amplifier and Noise Associated with Signal
The noise is random in nature, and it is accumulated at each amplification stage. Refer to Figure 4-2.
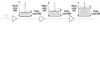 Figure 4-2 Noise
Accumulation Resulting from Multistage Amplification
Figure 4-2 Noise
Accumulation Resulting from Multistage Amplification
Amplifier noise is a severe problem in system design. A figure of merit here is the optical signal-to-noise ratio (OSNR) requirement of the system. The OSNR specifies the ratio of the net signal power to the net noise power. It is a ratio of two powers; therefore, if a signal and noise are both amplified, system OSNR still tells the quality of the signal by calculating this ratio. System design based on OSNR is an important fundamental design tool.
NOTE
OSNR is not just limited to optical amplifier-based networks. Other active and passive devices can also add noise and create an OSNR-limited system design problem. Active devices such as lasers and amplifiers add noise. Passive devices such as taps and the fiber can add components of noise. In the calculation of system design, optical amplifier noise is considered the predominant source for OSNR penalty and degradation. That does not imply unimportance to other sources of OSNR penalty.
Figures 4-1 and 4-2 shows the effect of noise on signal as the signal and noise pass through the amplifiers.
Dispersion, mentioned in Chapter 1, causes pulse spreading. The most important form of dispersion is group velocity dispersion (GVD). Group velocity is inversely proportional to the rate of change of propagation constant β with respect to frequency. Isn't β a constant? Not really! β actually (indirectly) depends on γ, the nonlinear coefficient, and P, the power of the signal. β further depends on the group index, which in turn depends on the GVD parameters. Therefore, dispersion causes severe pulse spreading and leads to intersymbol interference (ISI). The GVD parameter β2 is the second order differential of the β with respect to change in optical frequency-omega.
Techniques are available to compensate dispersion. Note here that the dispersion discussed so far (GVD) is called chromatic dispersion as opposed to other forms of dispersion, such as polarization mode dispersion, or PMD. (PMD is discussed from a design point of view in Chapter 5, "WDM Network Design -2".) Dispersion flattened or shifted fibers are an example. Dispersion shifted fibers (DSFs) have the zero-dispersion wavelength shifted into the operating band. Further dispersion-compensating fibers can be placed at strategic locations in a network so that we can reshape the broadened pulse as desired. Yet another technique is to use fine fiber Bragg gratings (FBGs)-based dispersion compensators. The question still remains: In a network, where do we place the dispersion compensators? Dispersion compensation is needed only for signals above a certain bit rate.
Another design issue is polarization. Assuming fibers to be polarization preserving is not a good idea. Different polarization states create different levels of PMD. PMD compensation and placement is yet another strong issue at high bit rate signals.
Last but not least, we need to consider fiber nonlinearities. Self-phase modulation and cross phase modulation are two common coupling problems. FWM, stimulated Raman scattering (SRS), and stimulated Brillouin scattering (SBS) are also high bit rate, high power issues.
A system design can be optimized by considering these effects in a strategic manner. The sections that follow consider several steps that need to be considered in an ideal system design case. Initially, let's assume a point-to-point link and then specifically look at ring and mesh networks in Chapter 5.