Time Error
So far, this chapter has outlined the mechanisms that help to synchronize a local clock to a given external reference clock signal. However, even when a local clock is determined to be synchronized in both phase and frequency to a reference clock, there are always errors that can be seen in the final synchronized clock signal.
These errors can be attributed to various factors such as the quality and configuration of input circuit being used as a reference; any environmental factors that influence the synchronization process; and the quality of oscillator providing the initial clock.
To quantify the error in any synchronized clock, various parameters have been defined by the standard development organizations (SDO). To understand the errors and the various metrics to quantify these errors, refer to Figure 5-13, which illustrates the output of a clock synchronized to an external reference clock. Because the measurement is taken from the synchronized clock that is receiving a reference signal, this synchronized clock will be referred to as the measured clock.
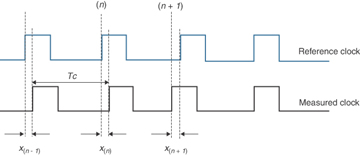
Figure 5-13 Comparing Clock Signals
It is also important to note that the error being referred to here is an error in significant instants or phase of a clock. This is called phase error, which is a measure of the difference between the significant instants of a measured signal and a reference signal. Phase error is usually expressed in degrees, radians, or units of time; however, in telecommunication networks, phase error is typically represented as a unit of time (such as ns).
The two main aspects that you need to keep in mind for understanding clock measurements are as follows:
Just as the measured clock is synchronized to a reference clock, the measured clock is always compared to a reference clock (ideally the same one). Therefore, the measurement represents the relative difference between the two signals. Much like checking the accuracy of a wristwatch, measurement of a clock has no meaning unless it is compared to a reference.
The error in a clock varies over time, so it is important that clock errors are measured over a sufficiently long time period to thoroughly understand the quality of a clock. To illustrate, most quartz watches gain/lose some time (seconds) daily. For such a device, a measurement done every few minutes or every few hours might not be a good indication of the quality. For such watches, a good time period might be one month, over which it could wander by up to (say) 10 seconds.
For illustration purposes, Figure 5-13 shows only four clock periods or cycle times, Tc, of a clock. These clock periods are shown as (n – 1), (n), and (n + 1). Notice that the measured clock is not perfectly aligned to the reference clock, and that difference is called clock error or time error (TE). The error is marked as x(n – 1) showing the error for instance (n – 1) of the clock period, x(n) for period (n), and so on. In the figure, the TEs at each successive instance of the clock period are marked as x(n – 1), x(n), and x(n + 1). The TE is simply the time of the measured clock minus the time of the reference clock.
In Figure 5-13, the measured clock signal at instance (n + 1) and (n) lags (arrives later than) the reference clock signal and is therefore by convention a negative time error. And for the interval (n + 1), the clock signal is leading the reference and is referred to as a positive time error. Of course, the time error measured at varying time periods varies and can be either negative or positive.
TE measurements in the time domain are normally specified in seconds, or some fraction of, such as nanoseconds or microseconds. As mentioned previously, there could be positive or negative errors, and so it is imperative to indicate this via a positive or negative sign. For example, a time error for a certain interval might be written as +40 ns, whereas another interval might be –10 ns.
An engineer can measure the TE value (against the reference) at every edge (or significant instant) of the clock over an extended observation interval. If these values are plotted in a graph against time on the horizontal axis, it might look something like the graph shown in Figure 5-14. Each additional measurement (+ or –) is added to the graph at the right. A value of zero means that for that measurement, the offset between the signals was measured as zero.
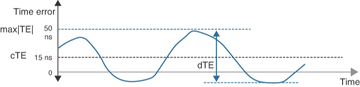
Figure 5-14 Graph Showing cTE, dTE, and max|TE|
This figure also includes several statistical derivations of TE, the main one being max|TE|, which is defined as the maximum absolute value of the time error observed over the course of the measurement. The following sections explain these measures and concepts. Refer to ITU-T G.810 and G.8260 to get more details about the mathematical models of timing signals and TE.
Maximum Absolute Time Error
The maximum absolute time error, written as max|TE|, is the maximum TE value that the measured clock has produced during a test measurement. This is a single value, expressed in units of seconds or fractions thereof, and represents the TE value that lies furthest away from the reference. Note that although the TE itself can be positive or negative, the max|TE| is taken as an absolute value; hence, the signed measured value is always written as a positive number. In Figure 5-14, the max|TE| is measured as 50 ns.
Time Interval Error
The time interval error (TIE) is the measure of the change in the TE over an observation interval. Recall that the TE itself is the phase error of the measured clock as compared to the reference clock. So, the change in the TE, or the TIE, is the difference between the TE values of a specific observation interval.
The observation interval, also referred to as τ (tau), is a time interval that is generally fixed before the start of a measurement test. The TE is measured and recorded at the beginning of the test and after each observation interval time has passed; and the difference between the corresponding time error values gives the TIE for that observation interval.
As an example, assuming an observation interval consists of k cycle times of a clock, the calculations for TE and TIE for the clock signals shown in Figure 5-15 are as follows (the measurement process starts at clock period n or (n)th Tc):
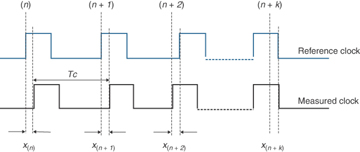
Figure 5-15 Time Error for k Cycle Periods as an Observation Interval
TE at (n)th Tc = difference between measured clock and reference = x(n)
TE at (n + 1)th Tc = difference between measured clock and reference = x(n + 1)
And similarly, TE at (n + k)th Tc = x(n + k) and so on
TIE for first observation interval (k cycles between n and n + k) = x(n + k) – x(n)
To characterize the timing performance of a clock, the timing test device measures (observes) and records the TIE as the test proceeds (as the observation interval gets longer and longer). So, if the clock period (Tc) is 1 s, then the first observation interval after the start of the test will be at t = 1 s, then the second will be at t = 2 s, and so on (assuming the observation interval steps are the same as the clock period).
This way, TIE measures the total error that a clock has accumulated as compared to a reference clock since the beginning of the test. Also, because TIE is calculated from TE, TIE is also measured using units of seconds. For any measurement, by convention the value of TIE is defined to be zero at the start of the measurement.
In comparison, the TE is the instantaneous measure between the two clocks; there is no interval being observed. So, while the TE is the recorded error between the two clocks at any one instance, the TIE is the error accumulated over the interval (length) of an observation. Another way to think of it is that the TE is the relative time error between two clocks at a point (instant) of time, whereas TIE is the relative time error between two clocks accumulated between two points of time (which is an interval).
Taking a simple example where the steps in the observation interval for a TIE measurement is the same as the period of a TE measurement, the TIE will exactly follow the contour of the TE. One case might be where the TE is being measured every second, and the TIE observation interval is increasing by one second at every observation. Although the curve will be the same, there is an offset, because the TIE value was defined to be at 0 at the start of the test.
Figure 5-16 shows this example case, where the plotted TIE graph looks the same as a plot of time error with a constant offset because the TIE value starts at 0. The list that follows explains this figure in more detail.

Figure 5-16 Graph Showing TE and TIE Measurements and Plots
As shown in Figure 5-16, the TE is +10 ns at the start of a measurement (TE0), at t = 0. Therefore, TE0 is +10 ns (measured), and the TIE is zero (by convention).
Assume that the observation interval is 1 second. After the first observation interval, from Figure 5-16, TE1 is 15 ns. The TIE calculated for this interval will be (TE1 – TE0) = 5 ns.
After the second observation interval, assume TE2 is 0 ns. The TIE calculated now will be (TE2 – TE0) = –10 ns. Note that this calculation is for the second observation interval and the interval for calculations really became 2 seconds.
The observation interval keeps increasing until the end of the entire measurement test.
There are other clock metrics (discussed later in this chapter), such as MTIE and TDEV, that are calculated and derived from the TIE measurements. TIE, which is primarily a measurement of phase accuracy, is the fundamental measurement of the clock metrics.
Some conclusions that you can draw based on plotted TIE on a graph are as follows:
An ever-increasing trend in the TIE graph suggests that the measured clock has a frequency offset (compared to the reference clock). You can infer this because the frequency offset will be seen in each time error value and hence will get reflected in TIE calculations.
If TIE graph shows a large value at the start of the measurement interval and starts converging slowly toward zero, it might suggest that the clock or PLL is not yet locked to the reference clock or is slow in locking or responding to the reference input.
Note that the measurement of the change in TE at each interval really becomes measurement of a short-term variation, or jitter, in the clock signals, or what is sometimes called timing jitter. And as TIE is a measurement of the change in phase, it becomes a perfect measurement for capturing jitter.
Now it is time to revisit the concepts of accuracy and stability from Chapter 1, “Introduction to Synchronization and Timing.” These are two terms that have a very precise meaning in the context of timing.
For synchronization, accuracy measures how close one clock is to the reference clock. And this measurement is related to the maximum absolute TE (or max|TE|). So, a clock that closely follows the reference clock with a very small offset is an accurate clock.
On the other hand, stability refers to the change and the speed of change in the clock during a given observation interval, while saying nothing about how close it is to a reference clock.
As shown in Figure 5-17, an accurate clock might not be a very stable clock, or a very stable clock might not be accurate, and so on. As the end goal is to have the most stable as well as the most accurate clock possible, a clock is measured on both aspects. The metrics that quantify both these aspects become the timing characteristics of a clock.
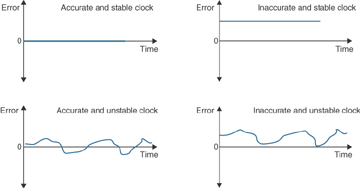
Figure 5-17 Considering Clock Accuracy and Stability
As you should know by now, the timing characteristics of a clock depend on several factors, including the performance of the in-built oscillator. So, it is possible to use that to differentiate between different classes of performance that a clock exhibits. Consequently, the ITU-T has classified clocks by the difference in expected timing characteristics—based on the oscillator quality. For example, a primary reference clock or primary reference source (PRC/PRS), based on a cesium atomic reference, is expected to provide better accuracy and stability when compared to a clock based on a stratum 3E OCXO oscillator. Chapter 3 thoroughly discussed these different classes of oscillator, so now it is time to define some metrics to categorize these qualities more formally.
Constant Versus Dynamic Time Error
Constant time error (cTE) is the mean of the TE values that have been measured. The TE mean is calculated by averaging measurements over either some fixed time period (say 1000 seconds) or the whole measurement period. When calculated over all the TE measurements, cTE represents an average offset from the reference clock as a single value. Figure 5-14 showed this previously, where the cTE is shown as a line on the graph at +15 ns. Because it measures an average difference from the reference clock, cTE is a good measure of the accuracy of a clock.
Dynamic time error (dTE) is the variation of TE over a certain time interval (you may remember, the variation of TE is also measured by TIE). Additionally, the variation of TE over a longer time period is known as wander, so the dTE is effectively a representation of wander. Figure 5-14 showed this previously, where the dTE represents the difference between the minimum and maximum TE during the measurement. Another way to think about it is that dTE is a measure of the stability of the clock.
These two metrics are very commonly used to define timing performance, so they are important concepts to understand. Normally, dTE is further statistically analyzed using MTIE and TDEV; and the next section details the derivations of those two metrics.
Maximum Time Interval Error
As you read in the “Time Interval Error” section, TIE measures the change in time error over an observation interval, and the TIE is measured as the difference between the TE at the start and end of the observation interval. However, during this observation interval, there would have been other TE values that were not considered in the TIE calculation.
Taking the example as shown in Figure 5-18, there were k time error values (k also being the observation interval). These time error values were denoted as x(n), x(n + 1), x(n + 2),…, x(n + k). The TIE calculation only considered x(n) and x(n + k) because the observation interval was k cycles starting at cycle n. It could be that these two values do not capture the maximum or minimum time error values. To determine the maximum variation during this time, one needs to find the maximum TE (x(max)) and minimum TE (x(min)) during the same observation interval.

Figure 5-18 TIE and MTIE Example
This maximum variation of the TIE within an observation interval is known as the maximum time interval error (MTIE). The MTIE is defined in ITU-T G.810 as “the maximum peak-to-peak delay variation of a given timing signal” for a given observation interval. As this essentially represents the variation in the clock, it is also referred to as the maximum peak-to-peak clock variation.
The peak-to-peak delay variation captures the two inverse peaks (low peak and high peak) during an observation interval. This is calculated as the difference between the maximum TE (at one peak) and minimum TE (another peak) for a certain observation interval. Figure 5-18 shows an example of TIE and of MTIE for the same observation interval, illustrating the maximum peak-to-peak delay variation.
The example in Figure 5-18 clearly shows that during an observation interval k, while the TIE calculation is done based on the interval between x(n) and x(n + k), there are peaks during this interval that are the basis for the MTIE calculations. These peaks are denoted by P(max) and P(min) in the figure.
Note also that as the MTIE is the maximum value of delay variation, it is recorded as a real maximum value; not only for one observation interval but for all observation intervals. This means that if a higher value of MTIE is measured for subsequent observation intervals, it is recorded as a new maximum or else the MTIE value remains the same. This in turn means that the MTIE values never decrease over longer and longer observation intervals.
For example, if the MTIE observed over all the 5-second periods of a measurement run is 40 ns, then this value will not go to less than 40 ns when measured for any subsequent (longer) periods. For example, any MTIE that is calculated using a 10-s period will be the same or more than any maximum value found for the 5-s periods. This applies similarly for larger values.
Therefore, MTIE can only stay the same or increase if another higher value is found during the measurement using a longer observation interval; hence, the MTIE graph will never decline as it moves to the right (with increasing tau).
The MTIE graph remaining flat means that the maximum peak-to-peak delay variation remains constant; or in other words, no new maximum delay variation was recorded. On the other hand, if the graph increases over time, it suggests that the test equipment is recording ever-higher maximum peak-to-peak delay variations. Also, if the graph resembles a line increasing linearly, it shows that the measured clock is not locked to the reference clock at all, and continually wandering off without correction. MTIE is often used to define a limit on the maximum phase deviation of a clock signal.
A simplified algorithm to record and plot MTIE is explained as follows:
Determine all the TE values for every 1-second interval (the values may have been sampled at a higher rate, such as 1/30 of 1 second).
Find the maximum peak-to-peak delay variation within each observed 1-s observation interval (MTIE values for 1-s intervals).
Record the highest value at the 1-s horizontal axis position in the MTIE graph.
Determine all the TE values for all 2-s intervals.
Find the maximum peak-to-peak delay variation within each observed 2-s interval (MTIE values for 2-s intervals).
Record the highest value against the 2-s horizontal axis position in the MTIE graph.
Repeat for other time intervals (4 s, 8 s, 16 s, etc.).
Figure 5-19 shows the MTIE limit for a primary reference time clock (PRTC), as specified in ITU-T G.8272.
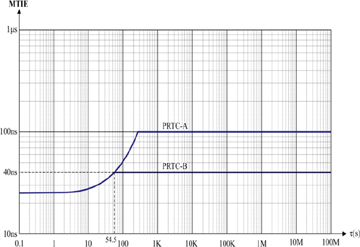
Figure 5-19 MTIE Limits for Two Classes of PRTC Clock (Figure 1 from ITU-T 8272)
The flat graph required by the recommendation for the MTIE values suggests that after a certain time period, there should not be any new maximum delay variation recorded for a PRTC clock. This maximum MTIE value, as recommended in ITU-T G.8272, is 100 ns for a PRTC class A (PRTC-A) clock and 40 ns for a PRTC class B (PRTC-B) clock. This line on the graph represents the limits below which the calculated values must remain and is referred to as a mask.
The standards development organizations have specified many MTIE masks—for example, the ITU-T has written them into recommendations G.812, G.813, G.823, G.824, and G.8261 for frequency performance of different clock and network types.
To summarize, MTIE values record the peak-to-peak phase variations or fluctuations, and these peak-to-peak phase variations can point to frequency shift in the clock signal. Thus, MTIE is very useful in identifying a shift in frequency.
Time Deviation
Whereas MTIE shows the largest phase swings for various observation intervals, time deviation (TDEV) provides information about phase stability of a clock signal. TDEV is a metric to measure and characterize the degree of phase variations present in the clock signal, primarily calculated from TIE measurements.
Unlike MTIE, which records the difference between the high and low peaks of phase variations, TDEV primarily focuses on how frequent and how stable (or unstable) such phase variations are occurring over a given time—note the importance of “over a given time.” This is important because both “how frequent” and “how stable” parameters would change by changing the time duration of the measurements. For example, a significant error occurring every second of a test can be considered a frequently occurring error. But if that was the only error that occurred for the next hour, the error cannot be considered to be a frequently occurring error.
Consider a mathematical equation that divides the total phase variations (TE values) by the total test time; you will realize that if there are less phase variations over a long time, this equation produces a low value. However, the result from the equation increases if there are more phase variations during the same test time. This sort of equation is used for TDEV calculations to determine the quality of the clock.
The low frequency phase variations could appear to be occurring randomly. Only if such events are occurring less often over a longer time can these be marked as outliers. And this results in gaining confidence in the long-term quality of the clock. Think of tossing five coins simultaneously, and with the first toss, all five coins come down heads! Without tossing those coins a lot more times, you cannot be sure if that was an outlier (a random event) or if something strange is wrong with the coins.
The TDEV of a clock defines the limit of any randomness (or outliers) in the behavior of a clock. The degree of this randomness is a measure of the low frequency phase variation (wander), which can be statistically calculated from TIE measurements and plotted on graphs, using a TDEV calculation.
According to ITU-T G.810, TDEV is defined as “a measure of the expected time variation of a signal as a function of integration time.” So, TDEV is particularly useful in revealing the presence of several noise processes in clocks over a given time interval; and this calculated measurement is compared to the limit (specified as a mask in the recommendations) for each clock type.
Usually, instability of a system is expressed in terms of some statistical representation of its performance. Mathematically, variance or standard deviation are usual metrics that would provide an adequate view to express such instability. However, for clocks, it has been shown that the usual variance or standard deviation calculation has a problem—the calculation does not converge.
The idea of convergence can be explained with a generic example. A dataset composed of a large collection of values with a Gaussian distribution will have a specific mean and variance. The mean shows the average value, and the variance shows how closely the values cluster around the mean—much like the stability of a clock. Now, if one were to calculate these values using a small subset or sample of these values, then the level of confidence in those metrics would be low—much like the toss of five coins. And as these parameters are calculated using larger and larger samples of this example dataset, the confidence in these metrics increases. The increase in confidence here means that variance moves toward a true value for the given dataset—this is referred to as convergence of variance. However, for clocks and oscillators, no matter how large the sample of variations is, apparently there is no evidence of this variance value converging. To deal with this deficiency, one of the alternative approaches is to use TDEV.
Rather than understanding the exact formula for calculating TDEV, it might be better to see the TDEV measure as a root mean square (RMS) type of metric to capture clock noise. Mathematically, RMS is calculated by first taking a mean (average) of square values of the sample data and then taking a square root of it. The key aspect of this calculation is that it averages out extremes or outliers in the sample (much more than the normal mean). Interestingly, the extremes average out more and more as the sample data increases.
Thus, TDEV becomes a highly averaged value. And if the noise in the clock is occurring rarely, the degree (or magnitude) of this rarely occurring error starts diminishing over longer periods of measurement. An example might be something occurring rarely or seldom, such as errors introduced by environmental changes over the course of the day (diurnal rhythms), such as the afternoon sun striking the exterior metal panel of the clock.
So, to gain confidence in the TDEV values (primarily to discard the rare noise occurrence in clock), the tests are usually quite long, at least several times longer than the usual MTIE observation intervals. For example, ITU-T G.811 calls for running TDEV tests for 12 times the maximum observation interval.
Compared to TDEV, you might notice that MTIE is perfectly suited to catch outliers in samples of TIE measurements. MTIE is a detector of peaks, but TDEV is a measure of wander over varying observation time intervals and is well suited to characterization of wander noise. It can do that because it is very good at averaging out short-term and rare variations.
So, it makes sense that TDEV is used alongside MTIE as metrics to characterize the quality of clock. As is the case for MTIE, ITU-T recommendations also specify TDEV masks for the same purpose. These masks show the maximum permissible values for both TDEV and MTIE for different clock types and in different conditions.
Noise
In the timing world, noise is an unwanted disturbance in a clock signal—the signal is still there, and it is good, but it is not as perfect as one would like. Noise arises over both the short term, say for a single sampling period, as well as over much longer timeframes—up to the lifetime of the clock. Because there are several factors that can introduce noise, the amount and type of noise can vary greatly between different systems.
The metrics that are discussed in this chapter try to quantify the noise that a clock can generate at its output. For example, max|TE| represents the maximum amount of noise that can be generated by a clock. Similarly, cTE and dTE also characterize different aspects of the noise of a clock.
Noise is classified as either jitter or wander. As seen in the preceding section “Jitter and Wander,” by convention, jitter is the short-term variation, and wander is the long-term variation of the measured clock compared to the reference clock. The ITU-T G.810 standard defines jitter as phase variation with a rate of change greater than or equal to 10 Hz, whereas it defines wander as phase variation with a rate of change less than 10 Hz. In other words, slower-moving, low-frequency jitter (less than 10 Hz) is called wander.
One analogy is that of a driver behind the wheel of a car driving along a straight road across a featureless plain. To keep within the lane, the driver typically “corrects” the steering wheel with very short-term variations in the steering input and force (unconsciously, drivers do these corrections many times per second). This is to correct the “jitter” of the car moving around within the lane.
But now imagine that the road is gently turning to the right and the driver is beginning to impact a little more force on the steering wheel in that direction to affect the turn. This is an analogy for wander. The jitter is the short-term variance trying to take you out of your lane, but the long-term direction being steered is wander.
The preceding sections explained that MTIE and TDEV are metrics that can be used to quantify the timing characteristics of clocks. Therefore, it is no surprise that the timing characteristics of these clocks based on the noise performance (specifically noise generation) have been specified by ITU-T in terms of MTIE and TDEV masks. These definitions are spread across numerous ITU-T specifications, such as G.811, G.812, G.813, and G.8262. Chapter 8 covers these specifications in more detail.
Because these metrics are so important, any timing test equipment used to measure the quality of clocks needs to be able to generate MTIE and TDEV graphs as output. The results on these graphs are then compared to one of the masks from the relevant ITU-T recommendation. However, it is imperative that the engineer uses the correct mask to compare the measured results against.
For example, if the engineer is measuring SyncE output from a router, the MTIE data needs to be compared to the SyncE mask from G.8262 and not from some other standard like G.812 (which covers SSU/BITS clocks).
Figure 5-20 represents the various types of categories of noise performance and the point at which they are relevant (and could be measured).
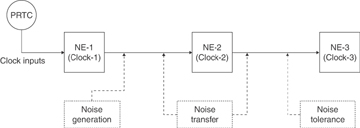
Figure 5-20 Noise Generation, Transfer, and Tolerance
The sections that follow cover each of these categories in more detail.
Noise Generation
Figure 5-21 illustrates the noise generation at the output of Network Element-1 (NE-1) and hence the measurement point for noise generation. Noise generation is the amount of jitter and wander that is added to a perfect reference signal at the output of the clock. Therefore, it is clearly a performance characteristic of the quality or fidelity with which a clock can receive and transmit a time signal. Figure 5-21 depicts some amount of noise that gets added and is observed at output, when an ideal (perfect) reference signal is fed to the clock.
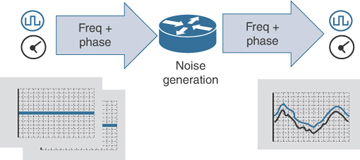
Figure 5-21 Noise Generation
One analogy that might help is that of a photocopier. If you take a document and run it though a photocopier, it will generate a good (or even excellent) copy of the document. The loss of quality in that process is an analogy for noise generation. But now, take a photocopy of that copy of the document, and a photocopy of that copy. Repeat that process, and after four to five generations of copies, the quality will have degraded substantially. The lower the noise generated in each cycle of the copy process, the more generations of copies can be made with acceptable quality.
For transport of time across a network, lower noise generation in each clock translates into a better clock signal at the end of the chain, or the ability to have longer chains. That is why noise generation is a very important characteristic for clocks.
Noise Tolerance
A slave clock can lock to the input signal from a reference master clock, and yet every clock (even reference clocks) generates some additional noise on its output. As described in the previous section, there are metrics that quantify the noise that is generated by a clock. But how much noise can a slave clock receive (tolerate) on its input and still be able to maintain its output signal within the prescribed performance limits?
This is known as the noise tolerance of a clock. Figure 5-20 shows the noise tolerance at the input of Network Element-3 (NE-3). It is simply a measure of how bad an input signal can become before the clock can no longer use it as a reference.
Going back to the photocopier analogy, the noise tolerance is the limit at which the photocopier can only just read the input document well enough to produce a readable copy. Any further degradation and it cannot produce a satisfactory output.
Like noise generation, noise tolerance is also specified as MTIE and TDEV masks for each class of clock performance. Up until the maximum permissible values of noise specified in ITU-T recommendations is applied at the input of a clock, the output of the clock should continue to operate within the expected performance limits. These masks are specified in the same ITU-T specifications that cover noise generation, such as G.812, G.813, G.823, G.824, and G.8262.
What happens when the noise at the input of a clock exceeds the permissible limits—what should be the action of a clock? The clock could do one or more of the following:
Report an alarm, warning that it has lost the lock to the input clock
Switch to another reference clock if there are backup references available
Go into holdover (operating without an external reference input) and raise an alarm warning of the change of status and quality
Noise Transfer
To synchronize network elements to a common timing source, there can be at least two different approaches—external clock distribution and line timing clock distribution.
An external clock distribution or frequency distribution network (refer to the section “Legacy Synchronization Networks” in Chapter 2, “Usage of Synchronization and Timing”) becomes challenging because the network elements are normally geographically dispersed. So, building a dedicated synchronization network to each node could become very costly, and hence this method is often not preferred.
The other approach is to cascade the network elements and use the line clocking (again refer to the section “Legacy Synchronization Networks” in Chapter 2), where the clock is passed from one network element to the next element, as in a daisy chain. Figure 5-20 shows the clock distribution model using the line clocking approach, where NE-1 is passing the clock to NE-2 and then subsequently to NE-3.
From the previous section on noise generation, you know that every clock will generate additional noise on the output of the clock compared to the input. When networks are designed as a daisy chain clock distribution, the noise generated at one clock is being passed as input to the next clock synchronized to it. This way, noise not only cascades down to all the clocks below it in the chain, but the noise gets amplified during transfer. To try to lessen that, the accumulated noise needs to be somehow reduced or filtered at the output of the clock (on each network element).
This propagation of noise from input to output of a node is called noise transfer and can be defined as the noise that is seen at the output of the clock due to the noise that is fed to the input of the clock. The filtering capabilities of the clock determines the amount of noise being transferred through a clock from the input to the output. Obviously, less noise transfer is desirable. Figure 5-20 shows the noise that NE-2 transferred to NE-3 based on noise it was subjected to from NE-1.
Again, as with the ITU-T clock specifications for noise generation and tolerance, MTIE and TDEV masks are used to specify the allowed amount of noise transfer. Remember that each clock node has a PLL with filtering capabilities (LPF and HPF) that can filter out noise based on the clock bandwidth (refer to the earlier section “Low-Pass and High-Pass Filters”).
The main metric used to describe how noise is passed from input to output is clock bandwidth, which was explained in the section “Low-Pass and High-Pass Filters.” For example, the noise transfer of an Option 1 EEC is described in clause 10.1 of ITU-T G.8262 as follows: “The minimum bandwidth requirement for an EEC is 1 Hz. The maximum bandwidth requirement for an EEC is 10 Hz.”